Square Root Of 100: Unlocking The Mystery In Simple Terms

Ever wondered what the square root of 100 really means? Well, buckle up, because we’re diving deep into this math concept that’s simpler than you think. You don’t need to be a math wizard to get it. In fact, by the end of this article, you’ll not only understand what the square root of 100 is but also how it applies to your everyday life. So, let’s break it down step by step, shall we?

Now, you might be thinking, “Why do I even need to know about square roots?” Great question! Believe it or not, square roots pop up in a lot of real-world scenarios—whether you’re calculating areas, solving equations, or just trying to impress your friends at a dinner party. And hey, who doesn’t love a good math fact?

So, without further ado, let’s jump right in. This article is your ultimate guide to understanding the square root of 100, breaking down the basics, exploring its applications, and answering some common questions along the way. Trust me, it’s gonna be a fun ride!

• Unveiling The Life Of Emely Peguero A Tale Of Resilience And Courage
• Exploring The Nationality Of Reece Walsh

What Exactly Is the Square Root of 100?

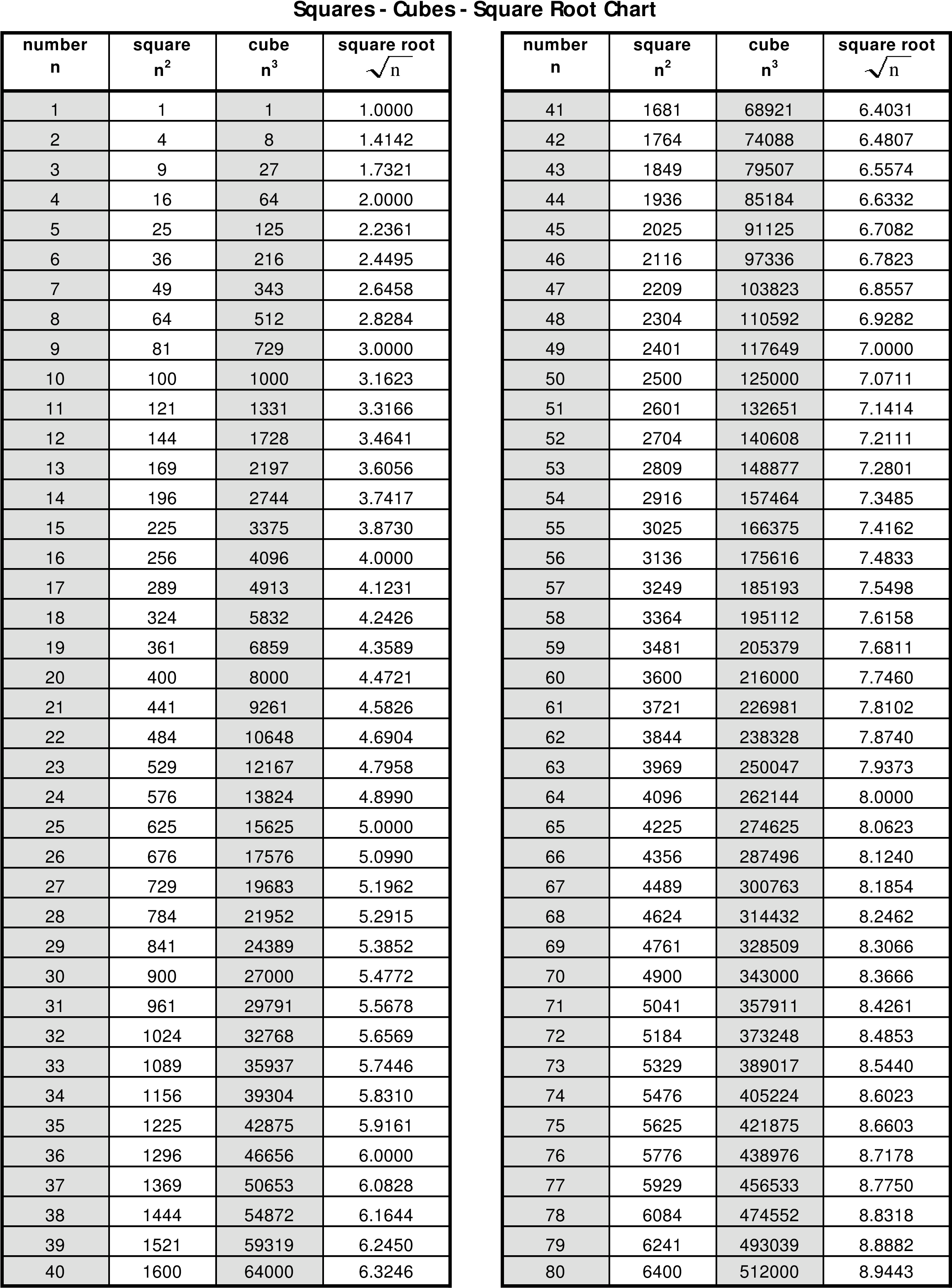
Let’s start with the basics. The square root of 100 is essentially the number that, when multiplied by itself, equals 100. Spoiler alert: that number is 10. Simple, right? But there’s a lot more to it than just crunching numbers.

Think of it like this: if you have a square with an area of 100 square units, the length of each side would be the square root of 100, which is 10. It’s all about balance and symmetry in math. Cool, huh?

Breaking It Down Further

Now, let’s take a closer look at how square roots work. Here are a few key points:

• Unveiling Alina Habbas Net Worth A Deep Dive Into Her Finances
• Unlocking The Secrets How To Check Website Keyword Ranking Effectively

• The square root of a number is always positive unless specified otherwise.
• Some numbers, like 100, have perfect square roots because they’re the result of multiplying an integer by itself.
• Not all numbers have perfect square roots. For example, the square root of 2 is an irrational number, meaning it goes on forever without repeating.

Understanding these fundamentals will help you grasp the concept of square roots better. And don’t worry, we’ll cover more examples later on.

Why Is the Square Root of 100 Important?

You might be wondering why the square root of 100 is such a big deal. Well, it’s not just a random number—it’s a cornerstone in mathematics and has practical applications in various fields. Let’s explore why it matters.

For starters, square roots are used in geometry to calculate distances, areas, and volumes. They’re also crucial in algebra, where they help solve quadratic equations. And let’s not forget physics, engineering, and computer science—all fields where square roots play a starring role.

Real-World Applications

Here are a few examples of how the square root of 100 (and square roots in general) is used in everyday life:

• Construction: Architects and builders use square roots to ensure structures are proportionate and stable.
• Finance: Investors use square roots to calculate risk and return on investments.
• Technology: Algorithms in computers rely on square roots for data analysis and processing.

As you can see, the square root of 100 isn’t just a theoretical concept—it’s a practical tool that affects many aspects of our lives.

How to Calculate the Square Root of 100

Calculating the square root of 100 is pretty straightforward, but let’s break it down step by step. First, you need to find a number that, when multiplied by itself, equals 100. In this case, that number is 10. Easy peasy, right?

But what if you don’t have a calculator or a computer handy? No worries! There are manual methods you can use, like the long division method or estimation techniques. Let’s take a look at these methods in more detail.

Long Division Method

The long division method is a classic way to calculate square roots. Here’s how it works:

1. Start by grouping the digits of the number into pairs, starting from the decimal point.
2. Find the largest perfect square less than or equal to the first group.
3. Subtract the square from the group and bring down the next pair.
4. Repeat the process until you reach the desired level of accuracy.

For 100, the process is simple because it’s a perfect square. But for other numbers, this method can be a bit more involved.

Common Misconceptions About Square Roots

There are a few misconceptions about square roots that we need to clear up. First, not all square roots are integers. In fact, most of them aren’t. For example, the square root of 2 is approximately 1.414, and it goes on forever without repeating.

Another common misconception is that square roots are always positive. While it’s true that the principal square root is positive, there’s also a negative square root for every positive number. For instance, the square root of 100 is both +10 and -10.

Clearing the Confusion

To avoid confusion, always specify whether you’re referring to the principal square root (positive) or both the positive and negative roots. This is especially important in algebra and higher-level math.

And remember, not every number has a perfect square root. Some numbers, like 100, are lucky enough to have one, but most don’t. That’s where approximation and estimation come in handy.

History of Square Roots

Believe it or not, square roots have been around for thousands of years. Ancient civilizations like the Babylonians and Egyptians used square roots in their calculations, long before calculators and computers were invented.

The concept of square roots evolved over time, with contributions from mathematicians like Pythagoras and Euclid. Today, square roots are a fundamental part of mathematics, and they continue to play a vital role in various fields.

Famous Mathematicians and Their Contributions

Here are a few mathematicians who made significant contributions to the study of square roots:

• Pythagoras: Known for the Pythagorean theorem, which involves square roots in its calculations.
• Euclid: Developed geometric methods for calculating square roots.
• Newton: Created iterative methods for approximating square roots.

These brilliant minds laid the foundation for modern mathematics, and their work continues to influence us today.

Fun Facts About Square Roots

Let’s spice things up with some fun facts about square roots:

• The square root of 0 is 0. Makes sense, right?
• The square root of 1 is 1. Simple but fascinating!
• Some numbers, like 100, have perfect square roots, while others, like 2, have irrational square roots.

Did you know that square roots are also used in art and music? Artists and musicians often use mathematical principles, including square roots, to create harmonious compositions. Cool, right?

Practical Examples of the Square Root of 100

Let’s look at some practical examples of how the square root of 100 is used in real life:

• Area Calculation: If you have a square room with an area of 100 square feet, the length of each side is the square root of 100, which is 10 feet.
• Physics: In physics, the square root of 100 might represent the velocity of an object after a certain period of time.
• Finance: Investors might use the square root of 100 to calculate the standard deviation of returns on an investment.

As you can see, the square root of 100 has a wide range of applications, making it a valuable concept to understand.

How to Use Square Roots in Everyday Life

Here are a few tips for using square roots in your daily life:

• Use square roots to calculate areas and distances.
• Apply square roots in budgeting and financial planning.
• Use square roots in DIY projects to ensure accuracy.

With a little practice, you’ll be using square roots like a pro in no time!

Common Questions About Square Roots

Let’s address some common questions people have about square roots:

• What is the square root of 100? The square root of 100 is 10.
• Can square roots be negative? Yes, but the principal square root is always positive.
• How do I calculate square roots manually? Use the long division method or estimation techniques.

These questions are just the tip of the iceberg when it comes to square roots. If you have more questions, feel free to ask in the comments below!

Conclusion: Why You Should Care About the Square Root of 100

So, there you have it—the square root of 100 explained in simple terms. Whether you’re a math enthusiast or just someone looking to understand the basics, square roots are a fascinating concept with practical applications in everyday life.

Remember, math isn’t just about numbers—it’s about solving problems and making sense of the world around us. By understanding the square root of 100, you’re taking a step toward becoming a more informed and capable problem solver.

Now, it’s your turn! Leave a comment below and let me know what you think. Do you have any questions or insights to share? And don’t forget to check out our other articles for more math tips and tricks.

Table of Contents

• What Exactly Is the Square Root of 100?
• Why Is the Square Root of 100 Important?
• How to Calculate the Square Root of 100
• Common Misconceptions About Square Roots
• History of Square Roots
• Fun Facts About Square Roots
• Practical Examples of the Square Root of 100
• Common Questions About Square Roots
• Conclusion: Why You Should Care About the Square Root of 100